Conspiracies
Take This
First things first, please go and take the Generic Conspiracist Beliefs Scale.
Read Up
Now go and read this short synopsis on this and other tests to assess what drives conspirators at Psychology Today1.
Data Files
Please download the files we’ll need.
Prerequisites
Like last week, open up Rstudio and create a new script by going to File > New File > R Script. Save this in an easily accessible folder. Now unzip this week’s data set and take the files - ConspiracyData.csv, ConspiracyCodebook.csv, ConspiracyMeasures.csv, and 04-walkthrough - and drop them all in a folder of their own. The Watkins (2018) article is a well written and handy guide to an otherwise dense statistical approach we’ll be using today.
Before we load the libraries, we’re going to grab a package called psych that is on CRAN. To install it, please run the following command in your console
install.packages("psych", dependencies = TRUE)
or you can simply use the dropdown menu by going to Tools > Install Packages and simply type in psych. Remember to have Install dependencies checkmarked!
If you would like to know more about the psych package and gain access to an extensive set of resources for personality and psychological tests, take a look at the Personality Project.
Now please go ahead and load up the following libraries or download and load if needed
library("tidyverse")
library("psych")
library("reactable")
library("polycor")
Then set the working directory to the location of the script by running
setwd(dirname(rstudioapi::getActiveDocumentContext()$path))
in your console or by selecting Session > Set Working Directory > To Source File Location.
Data Files
We’ll be looking at responses from a sample of 2449 people who took this test in 2016.
Loading a Local Data Set
To load the data set, codebook, and measures, run the following
conspiracy_data <- read_csv("ConspiracyData.csv")
## Rows: 2495 Columns: 15
## ── Column specification ────────────────────────────────────────────────────────
## Delimiter: ","
## dbl (15): Q1, Q2, Q3, Q4, Q5, Q6, Q7, Q8, Q9, Q10, Q11, Q12, Q13, Q14, Q15
##
## ℹ Use `spec()` to retrieve the full column specification for this data.
## ℹ Specify the column types or set `show_col_types = FALSE` to quiet this message.
conspiracy_codebook <- read_csv("ConspiracyCodebook.csv")
## Rows: 15 Columns: 2
## ── Column specification ────────────────────────────────────────────────────────
## Delimiter: ","
## chr (2): Item, Description
##
## ℹ Use `spec()` to retrieve the full column specification for this data.
## ℹ Specify the column types or set `show_col_types = FALSE` to quiet this message.
conspiracy_measures<- read_csv("ConspiracyMeasures.csv")
## Rows: 5 Columns: 2
## ── Column specification ────────────────────────────────────────────────────────
## Delimiter: ","
## chr (1): Description
## dbl (1): Measure
##
## ℹ Use `spec()` to retrieve the full column specification for this data.
## ℹ Specify the column types or set `show_col_types = FALSE` to quiet this message.
and take a look at each
conspiracy_codebook %>%
head()
## # A tibble: 6 × 2
## Item Description
## <chr> <chr>
## 1 Q1 The government is involved in the murder of innocent citizens and/or we…
## 2 Q2 The power held by heads of state is second to that of small unknown gro…
## 3 Q3 Secret organizations communicate with extraterrestrials, but keep this …
## 4 Q4 The spread of certain viruses and/or diseases is the result of the deli…
## 5 Q5 Groups of scientists manipulate, fabricate, or suppress evidence in ord…
## 6 Q6 The government permits or perpetrates acts of terrorism on its own soil…
conspiracy_measures
## # A tibble: 5 × 2
## Measure Description
## <dbl> <chr>
## 1 5 definitely not true
## 2 4 probably not true
## 3 3 not sure/cannot decide
## 4 2 probably not true
## 5 1 definitely not true
or to see a nicer table that is also interactive, you can use the reactable() command from the aptly named reactable package for a more Excel like feel and functionality.
reactable(conspiracy_measures)
reactable(conspiracy_codebook)
Well that is really long big and an annoyance if you want to find something. Let’s fix it by specifying the number of rows that appear and give it a search box.
reactable(conspiracy_codebook,
searchable = TRUE,
defaultPageSize = 3)
Now that is certainly better but if you don’t like it, just change the 3 in defaultPageSize = 3 to whatever you want.
Moving on, what if the data set is big? Then we might have an even bigger problem in how to display it. Let’s remind ourselves of the dimensions
dim(conspiracy_data)
## [1] 2495 15
That’s 2495 rows by 15 columns which is a pretty big data set and unlike the codebook, sometimes its nice to have options when it comes to looking at the number of rows and highlight the one I’m on. It may also be nice to save it as as something easier to recall like a word (aka a variable). You can probably see where this is going…
reactable(conspiracy_data,
searchable = TRUE,
defaultPageSize = 5,
showPageSizeOptions = TRUE,
highlight = TRUE)
That’s a bit better, though its certainly not perfect. There are a lot of things you can change about the table to make it easier to use. If you want to know more take a look at this vignette and some ways you can customize the tables. Don’t be scared off by the syntax. Remember its open source so just copy and paste. Eventually if you want to change certain aspects, just start tweaking what’s already there.
Method: Exploratory Factor Analysis (EFA)
Suppose you are conducting a survey and you want to know whether the items in the survey have similar patterns of responses, do these items hang out together to create a construct? This is the underlying principle of a factor analysis, or FA.
The basic assumption of a FA is that for a collection of observed variables, there are a set of underlying variables called factors which are smaller than those observed variables that can explain the interrelationships among those variables.
Moving forward, we’re going to conduct what is known as a single-factor exploratory factor analysis, or EFA. When you’re using this in the real world, be sure to use a dataset like this one, in that it only contains item responses in a numerical format - other types of data will cause errors and/or incorrect results. In the GCBS the scale is numeric so our dataset will do.
In a nutshell, an EFA is just a statistical method used to uncover underlying categorizations, groups, structures often hidden within a data set. This is done by assessing measures and could easily serve as your group level data! As a result, you can measure the internal reliability of a measure as well.
A Few Things
When you have an instrument with multiple scales, there are three standard approaches, of which we will only look at the last.
| EFA approach | Complexity | Retention | Description |
|---|---|---|---|
| Performed accounting for multiple scales | Most | Information is lossless | Between items of the same AND different scales |
| Performed on scales that have been reduced | Less | Information gathered from higher order scales is lost due to reduction | Between items of the same AND different scales at the lowest scaling |
| Performed on grouped items with like scales | Minimal | Only information between items with the same scaling is retained | Between items of the same scale |
Given that we’ll be only concentrating on the latter, you may have to run more than one EFA. After conducting the EFA, there are some things to consider if and when implementing your next one which we will cover at the end.
Example
Theoretically a five-point likert scale will have five underlying factors, or one for each choice. However in practice, this is rarely the case and we tend to treat the scale as an upper limit - ergo we can’t have more than five factors. So to decide on the number of factors, we use what is called a scree plot. Let’s do this for the first ten rows of our data set.
conspiracy_data_10 <-
conspiracy_data %>%
head(n=10)
scree(conspiracy_data_10)
## In smc, smcs < 0 were set to .0
## In smc, smcs < 0 were set to .0
## In smc, smcs < 0 were set to .0
## In factor.scores, the correlation matrix is singular, an approximation is used
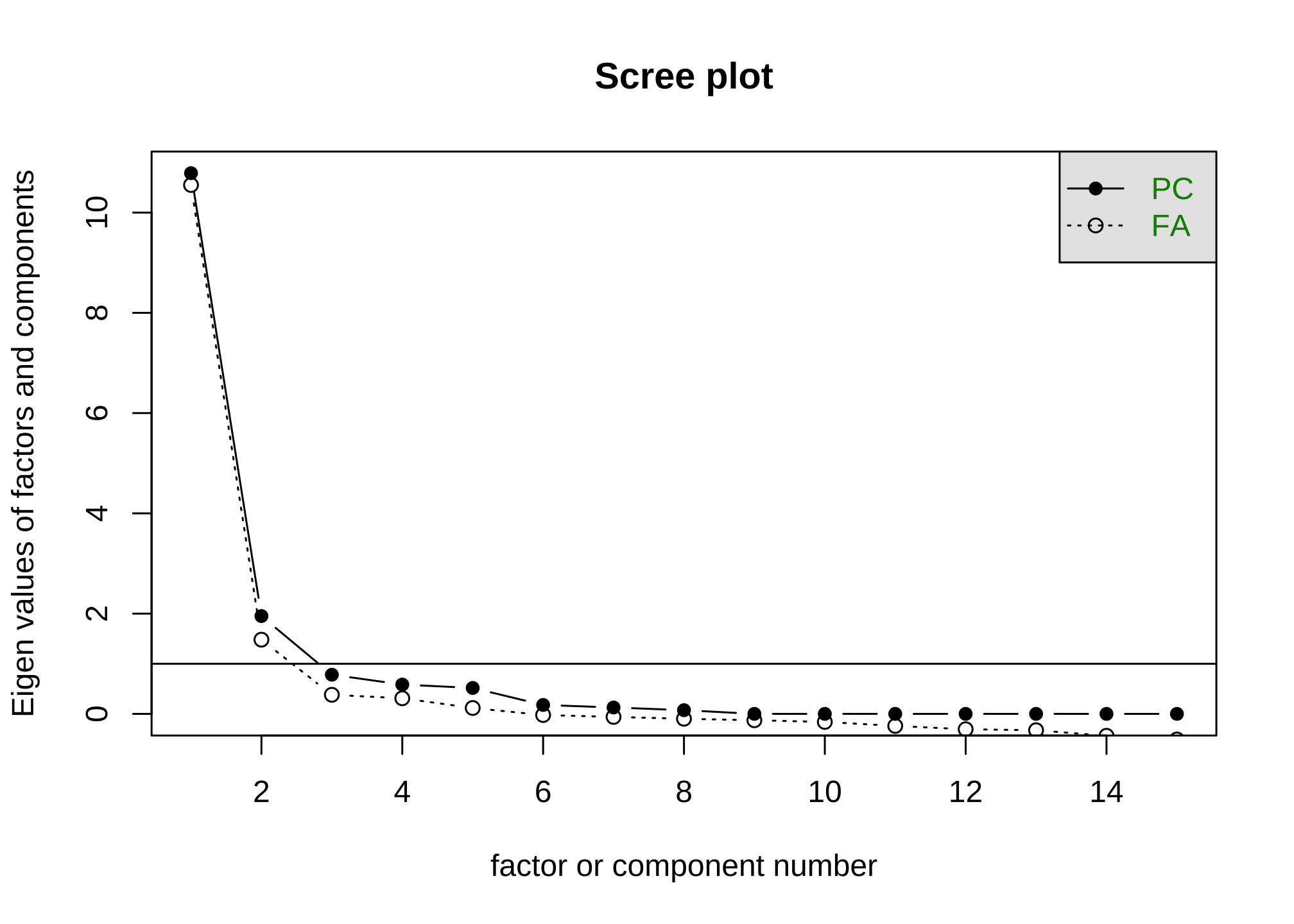
We’re going to ignore the y-axis and just look at where the open circle seems to cross that horizontal line. It looks like this happens around 3, so we can that there are likely three factors.
Conducting an EFA is relatively straight forward in R, and can be performed in any number of packages. In our case, we’ll use the popular psych package and the command fa() where we define the number of factors by nfactors.
EFA <-
fa(conspiracy_data_10,
nfactors = 3)
## In smc, smcs < 0 were set to .0
## In smc, smcs < 0 were set to .0
## In smc, smcs < 0 were set to .0
## Loading required namespace: GPArotation
## In factor.scores, the correlation matrix is singular, an approximation is used
and then to view the results
EFA
## Factor Analysis using method = minres
## Call: fa(r = conspiracy_data_10, nfactors = 3)
## Standardized loadings (pattern matrix) based upon correlation matrix
## MR1 MR2 MR3 h2 u2 com
## Q1 0.79 0.19 0.08 0.94 0.0613 1.1
## Q2 0.69 0.16 0.19 0.87 0.1253 1.3
## Q3 -0.01 0.93 -0.04 0.84 0.1636 1.0
## Q4 0.41 0.61 0.05 0.89 0.1061 1.8
## Q5 0.68 0.37 0.04 0.95 0.0497 1.5
## Q6 -0.02 -0.07 0.97 0.87 0.1318 1.0
## Q7 0.93 0.12 -0.06 0.94 0.0629 1.0
## Q8 0.15 0.78 0.03 0.80 0.2037 1.1
## Q9 0.71 -0.29 0.09 0.43 0.5680 1.4
## Q10 0.33 -0.12 0.77 0.99 0.0068 1.4
## Q11 0.92 -0.03 0.09 0.95 0.0501 1.0
## Q12 1.02 -0.10 -0.01 0.92 0.0760 1.0
## Q13 0.05 0.82 0.15 0.84 0.1632 1.1
## Q14 0.81 0.12 0.10 0.92 0.0754 1.1
## Q15 -0.06 0.17 0.94 0.94 0.0626 1.1
##
## MR1 MR2 MR3
## SS loadings 6.68 3.41 3.00
## Proportion Var 0.45 0.23 0.20
## Cumulative Var 0.45 0.67 0.87
## Proportion Explained 0.51 0.26 0.23
## Cumulative Proportion 0.51 0.77 1.00
##
## With factor correlations of
## MR1 MR2 MR3
## MR1 1.00 0.59 0.73
## MR2 0.59 1.00 0.31
## MR3 0.73 0.31 1.00
##
## Mean item complexity = 1.2
## Test of the hypothesis that 3 factors are sufficient.
##
## The degrees of freedom for the null model are 105 and the objective function was 165.97 with Chi Square of 525.57
## The degrees of freedom for the model are 63 and the objective function was 140.43
##
## The root mean square of the residuals (RMSR) is 0.04
## The df corrected root mean square of the residuals is 0.05
##
## The harmonic number of observations is 10 with the empirical chi square 3.45 with prob < 1
## The total number of observations was 10 with Likelihood Chi Square = 163.84 with prob < 6.5e-11
##
## Tucker Lewis Index of factoring reliability = -0.896
## RMSEA index = 0.386 and the 90 % confidence intervals are 0.343 0.501
## BIC = 18.77
## Fit based upon off diagonal values = 1
Viewing and Visualizing Factors
Each result using the fa() command actually gives you a list, and each element of the list contains specific information about the analysis, including factor loadings. Factor loadings represent the strength and of the relationship between each item and the underlying factor, and they can range from -1 to 1. We can see this by looking only at the first column
EFA$loadings
##
## Loadings:
## MR1 MR2 MR3
## Q1 0.786 0.194
## Q2 0.686 0.164 0.189
## Q3 0.934
## Q4 0.414 0.613
## Q5 0.685 0.371
## Q6 0.966
## Q7 0.935 0.115
## Q8 0.151 0.782
## Q9 0.712 -0.287
## Q10 0.331 -0.116 0.774
## Q11 0.924
## Q12 1.025
## Q13 0.825 0.149
## Q14 0.811 0.125
## Q15 0.175 0.944
##
## MR1 MR2 MR3
## SS loadings 5.809 2.913 2.521
## Proportion Var 0.387 0.194 0.168
## Cumulative Var 0.387 0.581 0.750
You can also create a diagram of loadings. The fa.diagram() command takes the output from fa() and creates a diagram, called a path diagram to show the items’ loadings ordered from strongest to weakest. This type of visualization can be a helpful way to represent your results where the factor loading are represented on the arrows going from each factor to their respective items.
fa.diagram(EFA)
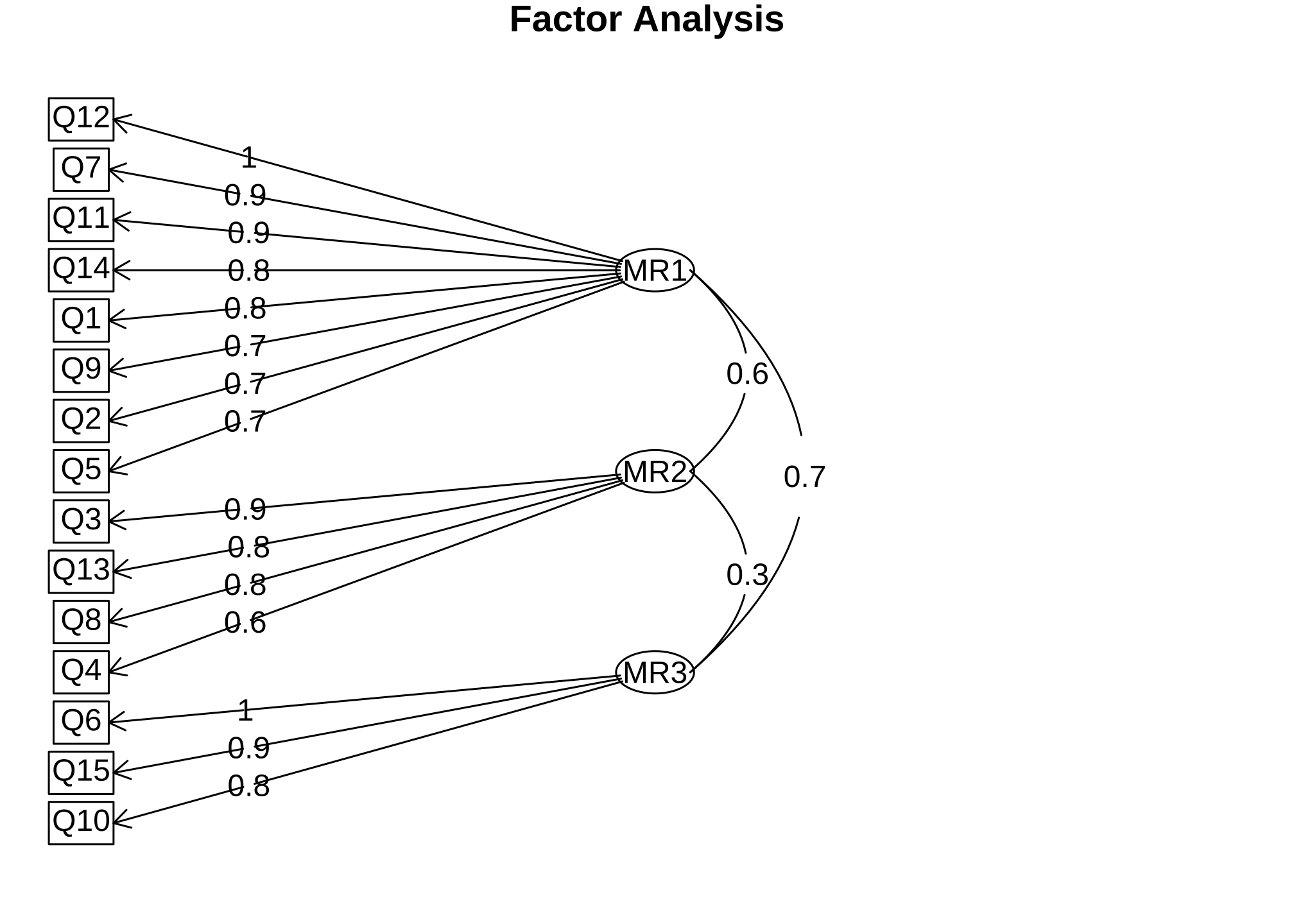
For those of you who have some statistical background, factor loadings show the correlation between the observed score and the latent score. Generally, the higher the better since the square of factor loading can be directly translated as item reliability. The other number between the factors is called a factor correlation that I am definitely not going to cover here other than to say that it tells us how well the factors correlate with each other. Since you are just learning about EFAs, disregard both of these for right now and just focus on the underlying concept of a factor and possibly think about how amazing it is that an algorithm and statistical approach can group variables together simply from raw response data.
What if you only have a single factor?
A single factor tells you that your items likely fit onto a single theoretical construct which is just a fancy way of saying a single category. Operationally that means they can be represented on one dimension/scale which is nice and easy, but you can’t get much information out of the items beyond what they tell you individually. But this is not necessarily a bad thing and you can use the output to your advantage, in that you can
use the factor analysis to help refine your scale like choosing only those items with higher loadings on the factor and removing those that are lower - i.e. by using some threshold to separate the higher values from the lower values you see on the arrows going from the factor to the items.
see if any of your items could be reverse-scored on the scale by determining any negative loadings on the factor - i.e. negative values you see on the arrows going from the factor to the items.
Side Note: Lack of Pipes
So why can’t we just use pipes and ggplot here? Well the main problem can be found using this command
class(EFA)
## [1] "psych" "fa"
Notice that the psych package has its own data type called “psych”. Tidy involves data that is neatly in rows and columns. In any case, we’ll stick to the default format for now.
You can actually use the class() syntax to figure out the data type for any variable in R.
Anyway getting back to the issue, we have three factors consisting of certain items. Now the final step is to go back and decide compartmentalize MR1, MR2, and MR3 based on how the questions are grouped.
Interpreting Factor Scores
…using Items
Let’s take a look at the codebook, but this time look at them by items within factors
MR1_factor <-
conspiracy_codebook %>%
filter(str_detect(Item, paste(c("Q12", "Q7", "Q11", "Q14", "Q1", "Q9", "Q2", "Q5"), collapse = '|')))
MR2_factor <-
conspiracy_codebook %>%
filter(str_detect(Item, paste(c("Q3", "Q13", "Q8", "Q4"), collapse = '|')))
MR3_factor <-
conspiracy_codebook %>%
filter(str_detect(Item, paste(c("Q6", "Q15", "Q10"), collapse = '|')))
If you’re interested, the | is called a logical operator and it means the word or. Information about other operators can be found here.
reactable(MR1_factor,
defaultPageSize = 11)
reactable(MR2_factor)
reactable(MR3_factor)
We could say that
MR1= information control by groupsMR2= hiding information from the publicMR3= acts of self-interest to suppress information
Of course there are many interpretations so yours may differ. Regardless the idea should always be in the context of your original purpose and research questions.
The additional benefit here is that these interpretations can serve as natural groupings, or ones that are derived from, rather than labeling them prior to a statistical analysis.
…using Participants
An EFA contains information about factor scores for each participant in your data set These scores are indicators of how much or how little of the factor each participant likely possesses. Please note that factor scores are not calculated for respondents with missing data. That issue will be tackled in next week’s walkthrough. Anyway let’s take a look at our data by calculating the total scores.
To see an example, lets first look at the raw data for the first six participants
head(conspiracy_data_10)
## # A tibble: 6 × 15
## Q1 Q2 Q3 Q4 Q5 Q6 Q7 Q8 Q9 Q10 Q11 Q12 Q13
## <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
## 1 5 5 3 5 5 5 5 3 4 5 5 5 3
## 2 5 5 5 5 5 3 5 5 1 4 4 5 4
## 3 2 4 1 2 2 2 4 2 2 4 2 4 0
## 4 5 4 1 2 4 5 4 1 4 5 5 5 1
## 5 5 4 1 4 4 5 4 3 1 5 5 5 3
## 6 1 1 1 1 1 1 1 1 1 1 1 1 1
## # … with 2 more variables: Q14 <dbl>, Q15 <dbl>
or if you prefer, we can show this using
reactable(conspiracy_data_10)
We can then apply rowSums() command to see the total scores for these respondents.
conspiracy_data_10 %>%
head() %>%
rowSums()
## [1] 68 65 37 55 59 15
Then let’s look at the first six participant factor scores to see the relationship between those and the responses.
head(EFA$scores)
## MR1 MR2 MR3
## [1,] 0.9424517 0.8902524 0.7404219
## [2,] 0.7800917 1.8475388 0.1314532
## [3,] -0.1400622 -0.8264001 -0.2598484
## [4,] 0.8861106 -0.9053159 0.8159931
## [5,] 0.8020422 0.1576844 0.8300740
## [6,] -1.3316336 -0.7584980 -1.6976942
and with their descriptive summary
summary(EFA$scores)
## MR1 MR2 MR3
## Min. :-1.3316 Min. :-0.9210 Min. :-1.6977
## 1st Qu.:-1.0170 1st Qu.:-0.8094 1st Qu.:-0.2542
## Median : 0.3200 Median :-0.3004 Median : 0.3749
## Mean : 0.0000 Mean : 0.0000 Mean : 0.0000
## 3rd Qu.: 0.8336 3rd Qu.: 0.6661 3rd Qu.: 0.7523
## Max. : 0.9425 Max. : 1.8475 Max. : 0.8301
I can plot the density curve
plot(density(EFA$scores,
na.rm = TRUE),
main = "Factor Scores")
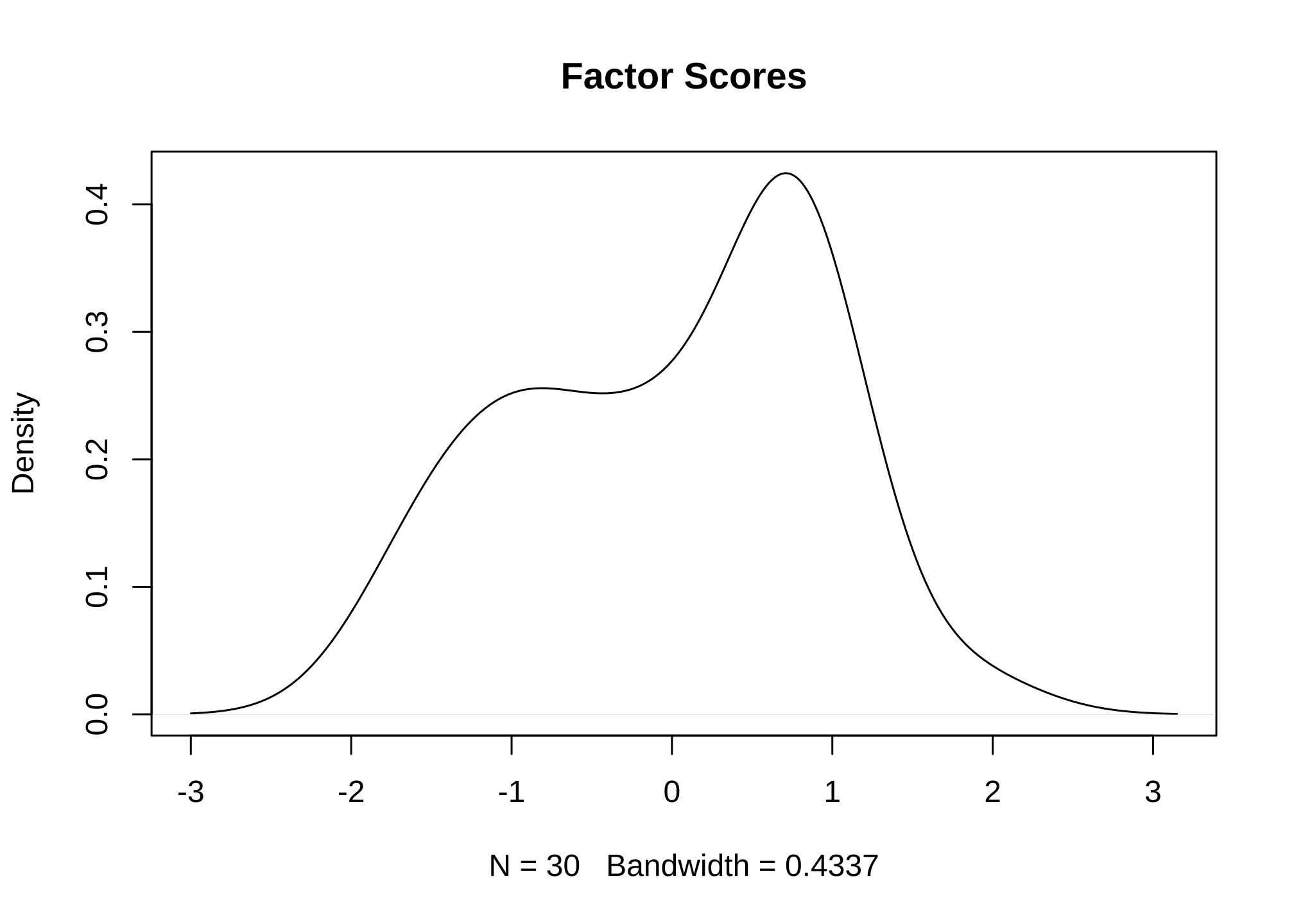
to get a feel for how the data looks. So what does it all mean with respect to the larger data set? Well nothing because EFAs only apply to the data that was used. This was an example of how to go about performing one so we used a very small subset of the entire population for the purposes of showing an example. To administer a proper one, we would go back and perform it on the entire 2449 row data set. In fact, as a general rule of thumb, you should always perform an EFA in your entire data set unless there is an underlying reason not to.
Additional Things
Even though we looked at how factors apply at to the participants, you should know that interpretations aren’t conducted at the individual level. This means creating overarching statements about any of these ten participants separately would be complete nonsense. However the benefit is when conducting one using a subset of a large data, you get information in the form of indicators - or to put it another way you get an idea of what an EFA on the entire data set may tell you. If you do this, just make sure to use a large enough random sample of the participants instead of what I did in the example.
If you want to know what the study said broadly, please take a look over the Brotherton, French & Pickering (2013) paper.
Caveaut
OK so we’ve conducted an EFA, but what I didn’t tell you is that there are some guidelines to think about before implementing one. For those who have not had a statistics course may consider skipping the first for now, though the basic idea of the variance is given in this footer2
- Each factor must only contain items explaining at least 10% of the variance in its respective factor.
- Each factor is recommended to have at least three items.
- Each factor must be interpreted in a reasonable and applicable way.
- It is recommended that your factoring do not have items that appear in multiple factors with a similar factor loading.
Let’s Stop Here
OK that’s enough. EFAs can be quite useful, but due to the complexity of the approach they can be misused or misinterpreted. While no doubt still difficult, hopefully the walkthrough provided some grounded explanations of how they are used and what you can with the results. A lot of the additional assumptions, benefits, possible outcomes, side effects, etc have been set aside for the purposes of simplifying this approach. I encourage you to further explore EFAs and after you get “comfortable” with them, take a look at the idea of a confirmatory factor analysis (CFA) as well. Warning that CFAs lead down a rabbit hole into some higher level statistics!
Looking Forward
Recall that a factor analysis can only be performed on a full set of data, but what if you don’t have that? Its something we deal with all of the time and we’ll talk about how to deal with missingness next week!
I am personally fond of the BSR. ↩︎
We essentially want a way to describe the spread of our data from one end to another, or dispersion. We have some ways to do this such as mean, median, and mode but that doesn’t tell us the whole picture since these are just ways to describe the average. They essentially do not say anything about how far away from the mean, median, or mode is from the raw data since that varies - ergo the term variance. ↩︎